Physics-Informed Neural Networks and Classical Numerical Methods

In the field of artificial intelligence, a groundbreaking concept has emerged. It’s called Physics-Informed Neural Networks (PINNs). These are gaining attention because they can combine traditional physics-based approaches with modern neural networks. This fusion of physics principles and machine learning is poised to transform various industries.

Table of Contents

What are Physics-Informed Neural Networks (PINNs)?

Physics-Informed Neural Networks (PINNs) represent a groundbreaking approach that merges the accuracy of physics-based modeling with the flexibility of neural networks. Traditional physics-based models often struggle with complex real-world scenarios due to their reliance on simplifying assumptions. Neural networks, on the other hand, excel at learning patterns from data but lack the foundational understanding of physical laws. PINNs aim to strike a balance by integrating physical equations directly into neural networks, allowing them to capture intricate relationships while adhering to fundamental laws.

Advantages and Benefits

Enhanced Generalization: By incorporating physical principles, PINNs improve their ability to generalize from limited data. This is particularly useful in scenarios where data is scarce or expensive to obtain.
Combining Data and Knowledge: PINNs enable the fusion of experimental data and domain expertise, resulting in models that are both data-driven and physics-informed.
Adaptability: These networks can adapt to new data while staying grounded in the underlying physics. This adaptability is crucial for systems affected by changing conditions.
Reduced Computational Cost: PINNs often require fewer simulations than traditional physics-based methods, leading to significant savings in computational resources.
Multi-Disciplinary Applications: From fluid dynamics and materials science to medical imaging and finance, PINNs find applications in diverse fields due to their ability to handle complex, multi-disciplinary problems.

Challenges and Future Directions

While the potential of PINNs is exciting, challenges remain. Integrating complex physics equations into neural networks requires careful architecture design and training strategies. Ensuring PINNs maintain their accuracy while scaling to more extensive datasets is an ongoing research focus in scientific machine learning. Moreover, expanding the framework to include uncertainty quantification and robustness is essential for real-world deployment.

PINNs (Physics-Informed Neural Networks) revolutionize our approach to intricate challenges requiring a fusion of physics comprehension and machine learning skills in the realm of scientific machine learning. As researchers delve further into honing PINN architecture, training techniques, and applications, we anticipate these networks will revolutionize industries and unveil solutions that were once unattainable. Whether enhancing industrial processes or propelling medical diagnostics, PINNs possess the power to shape the future and redefine the boundaries of possibility at the crossroads of AI, physics, and scientific machine learning.

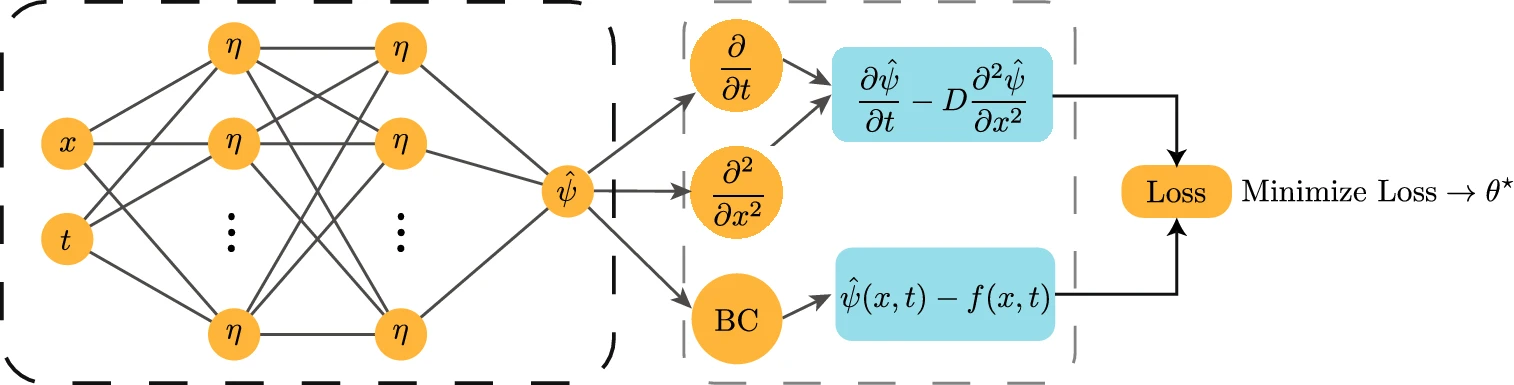
Recently, two intriguing papers have been published that aim to reconcile classical methods, specifically the finite difference method, with physics-informed neural networks. These papers are worth a read.

Weight initialization algorithm for physics-informed neural networks using finite differences
Physics Informed Neural Network using Finite Difference Method

These two papers attempt to reconcile the classical finite difference method with Physics-Informed Neural Networks (PINNs).

The first paper integrates a finite difference solution to enhance the training loss of PINNs and introduces an innovative approach to decrease the computational training cost of the PINNs. The second paper employs the finite difference method in lieu of automatic differentiation.

Furthermore, there are papers debating the dominance of physics-informed neural networks.

What are some other interesting papers you have encountered?

The source of this short post is this¹ reddit post.